この記事に共感したら
チョコレートを最短で12個に分けるには？注意深く考えて！ 算数脳（15）【連載】
公開
更新
AI化が進むなかで、論理的思考を身につけておくことはとても大切。社会人の素養としても必須の数学的思考を育てるパズルで、「できる脳」を育てましょう。単なる知識を超え、論理的思考力と柔軟な発想力を鍛えるパズルに、ぜひ挑戦してみてください！
※この記事は『頭のいい小学生が解いている算数脳がグンと伸びるパズル』（松永暢史・星野孝博/KADOKAWA）からの抜粋です。
チョコ割り計算
下のチョコレートを溝（みぞ）にそって、12 個に割ろうと思います。何回で12 個に割れるでしょうか？ もっとも少ない回数を答えてください。ただし、割ったものを重ねたり、並べたりして、いっしょに割ってはいけません。
☆割り方は、答えに関係ありません。
（スクロールすると答えがあらわれます）
【答え】11 回
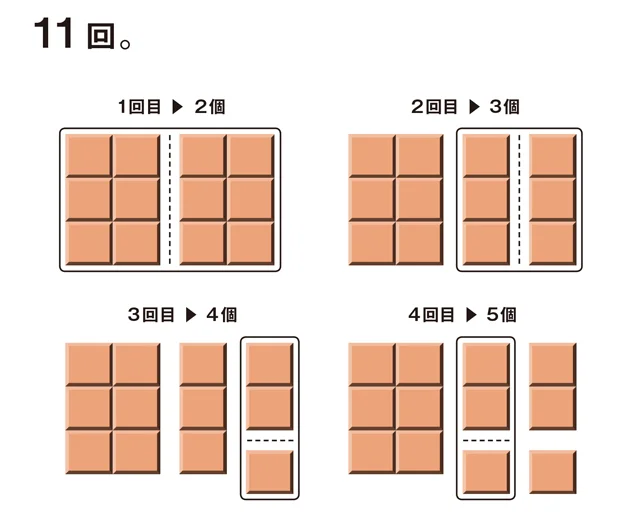
解説
いろいろな割り方があるので、一見すると、とてもむずかしい問題に思われる方も多いでしょう。
問題文の「もっとも少ない」という言葉に気を取られず、割ることによるチョコレートの数の変化に着目すれば、どのように割っても同じ回数になることに気づくでしょう。
解説図の線で囲まれた部分が、その回で割られるチョコレートですが、その部分だけ見れば、いつも1 つのチョコレートが2 つになっています。割られたもの以外の数は変わらないので、全体の数は1 回割るごとに1 つ増えることがわかります。
そしてチョコレートの数は、割る回数より1大きい数になっているので、11 回目に12個となることがわかります。
この問題では「注意型発想力」と「分析型発想力」を同時に使います。割るということと、チョコレートの数の関係をじっくり考えることが重要です。
Information
『頭のいい小学生が解いている算数脳がグンと伸びるパズル』
これからの受験を乗り切るためには、論理的思考ができる数学能力が大切。単なる知識を超えた、論理的思考力と柔軟な発想力を育てるには、パズルが効果的です。大人にも挑戦しがいのあるパズルを全101問取り揃えました。
▼掲載話一覧はこちら
著者：松永暢史（まつなが・のぶふみ）
1957年生まれ。慶應義塾大学文学部卒業。教育環境コンサルタント。教育や学習の悩みに応えるV-net主宰。「受験のプロ」として音読法や作文法、サイコロ学習法などを開発し、執筆や講演などで活躍。『男の子を伸ばす母親は、ここが違う!』『ガミガミ言わずに子どもを勉強させる方法』など著書多数。
星野孝博（ほしの・たかひろ）
1970年、愛知県出身。東京理科大数学科卒業。日本パズル協会代表理事。日本で唯一、教育的メカニカルパズルを専門に扱う（株）クロノス代表取締役。パズル制作のほか、パズルショップやクロノスパズル教室の運営を行う傍ら、Eテレアニメ『ファイ・ブレイン~紙のパズル~』の監修などにも携わるなど幅広く活躍。
本ページはアフェリエイトプログラムによる収益を得ています
おすすめ読みもの(PR)
プレゼント応募
プレゼント企画
「「NANOX one PRO・ソフラン プレミアム消臭 汗臭ブロック…」
頑固な汚れ、気になる汗臭に！ お洗濯の最強コンビ
メルマガ登録で毎週プレゼント情報が届く!
新規会員登録する
読みものランキング
-
1位お尻から大量出血でトイレがすごいことに！病院を後回しにしていたら…／痔だと思ったら大腸がんステージ4でした（1）
-
2位「理想の人がいるなんて幻想、今すぐ捨ててください」結婚相談所で受けた非情な宣告／結婚さえできないわたし 29歳からの婚活地獄（1）
-
3位「うちの子に限って」いじめへの関与なんて絶対ありえないと思っていたのに／娘がいじめをしていました（1）
-
4位ヤバくて有名な「クレクレ友人」に翻弄される物語。軽い気持ちのSNS投稿が…／欲しがるあの子を止められない（1）
-
5位小5の夏に経験した親友の失踪。20年後に出会ったのは、彼女にそっくりな女性で／その叫びは聞こえていたのに（1）
読みものランキングをもっと見る
レシピランキング
レシピランキングをもっと見る
レタスクラブ最新号
レタスクラブ最新号詳細